|
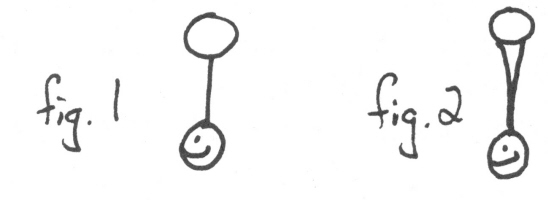
THE BALLANCE -- A THEORETICAL MINI-DISSERTATION The comments on juggling theory by Richard Morganti in the October-November 1977 Newsletter got me thinking: The term "double-balance" has been loosely applied to assorted spinning and balancing feats. Most jugglers have assumed that any true double-balance feat without gimmicks is patently impossible. But is it? I will employ an example to show how this argument encounters theoretical difficulties. Superficially considered, the balancing feat in figure 1 would be regarded as impossible. Hence a tapering conical extension is used on the upper end of the stick as in figure 2, allowing the ball to "rest" in the resulting concavity.
This
way the juggler is only responsible for a single "point of
balance", at the point where the stick rests on the forehead. The
problem is with how one defines "rest" and "point of
balance". It is only slightly less difficult to balance a ball in
this fashion with an open-ended cone one-half the diameter of the ball
(figure 3) than it is using a cone onefourth the diameter of the ball.
(Figure 4) .
The
ball is still said to be "resting" on the cone in either case.
With still smaller cones, the ball can be more precariously
"rested", or as some would say, "balanced". Where
the individual balancer defines this difference for practical purposes
depends upon his proficiency. A sufficiently steady balancer could do
the trick in figure 1 with a 40 cm. sphere and a 2 em. stick, if he hollowed out the end of the stick just enough to perfectly match the curvature of the ball:
The theoretical meat of this issue is the interaction due to gravity between perfectly planar and spherical surfaces. In
the above example, the ratio of the diameters of the cone top and the
sphere decreased from 20/40 cm (1/2) to 2/40 cm
Working only with perfect planes and spheres on theoretical grounds, we can formulate the following definition: When one sphere's center of gravity is directly over a single point of that sphere's contact with a plane or oppositely-curving sphere, it is said to be balanced. Thus, figures 7 and 8 would be good balances, but figure 9 would not be.
The balancer will gain an appreciation for this definition if he first tries the trick in figure 8 with a plank of wood and a rubber ball, and then with a plane of plate glass and a crystal ball. The latter is considerably more difficult because it more closely approximates geometrically ideal conditions. However little all this may apply to real life balancing, the performer should be aware of the theoretical basis of his act. --David Low, Providence, RI
|