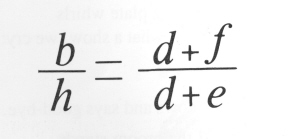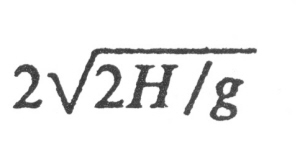By Joe Buhler and Ron Graham

 

Jugglers around the world make millions of upward tosses daily without ever considering why objects fall back into their hands. For those not capable or caring enough to figure it out, the two juggling mathematicians who wrote this article have described the ultimately important mechanics of this

pure motion. All the everyday juggler need remember is:

(The following information on the kinematics of juggling is excerpted from a longer article that Buhler and Graham have written for publication in La Recherche, a French scientific journal.)

 

The essence of juggling is the stabilization of a pattern by using feedback to accommodate and correct minor variations. Some possible sources of variation are obvious - throws that have slightly incorrect destinations or slightly incorrect heights. Another important variable is the timing of the throws.

 

Jugglers instinctively learn that there are con­straints placed on their patterns by the necessity of timing the throws correctly. If a ball is thrown too late another ball drops (the performer's nightmare) and if it is thrown too early the pattern can degenerate quickly into instabilities that can not be dampened.

 

In order to quantify some of these constraints we will consider an idealized juggling pattern.

 

Suppose that a pattern has a fixed number of hands and balls and that it is such that each ball follows the same path, each ball takes the same time in flight, and each ball spends the same amount of time in a hand. More precisely the following five quantities are all assumed to be constant:

 

b: the number of balls

h: the number of hands

f: the flight time of each balI between hands

e: the empty time - the time a hand is empty between balls

d: the dwell time - the time each ball spends in a hand.

 

Furthermore we assume, for the convenience of exposition, that two balls are never in the same hand at the same time and that the pattern is periodic in the sense that each configuration reoccurs at fixed time intervals.

 

These assumptions imply that the juggling pattern has a certain symmetry and uniformity in addition to a stable pattern and rhythm. The cascade is an example of a pattern for which these assumptions are valid, and the shower is an example for which the assumptions are not valid. These ideas can be generalized to yield (somewhat more complicated) results in the absence of these assumptions; any pattern can be analyzed.

 

The basic relationship is:

 b/h = (d+f) / (d+e)

 

This should be regarded as a constraint that interrelates the above variables. It would be. nice to call this result Shannon's Theorem since it is due to the mathematician Claude Shannon, but several of the seminal results in coding and information theory already bear that name.

 

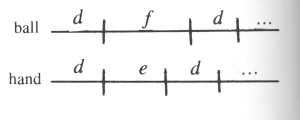
It is not too hard to see why something like this must be true. Consider one period of the "time line" of the typical hand and typical ball:

 

 

 

 

 

 

Here d denotes an interval in which the ball is in a hand. f denotes an interval in which the ball is in flight, and e denotes the interval in which the hand is empty. Thus, if a hand holds m balls in one period of the pattern and a ball visits n hands in a period, then the total number of ball/hand contacts can be counted in two ways; we deduce that:  bn=hm

 

The total period length can be computed In two ways - either by looking at the ball time­line or the hand time-line. The result is that

 

The flight time f is directly related to the height of a throw so that this result can also be regarded as a constraint on the height of a throw.

 

Indeed, the height of a throw uniquely determines its flight time. If a ball follows a parabolic path and is thrown to height H. then the ball takes time