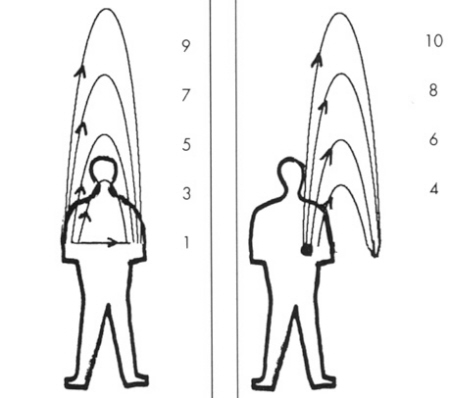
Figure
1- (left) The odd throws cross sides. The 1 throw is handed directly
from hand to hand. Figure 2- (right) The even throws land in the same hand that threw them. A tossed 2 would go up only two inches. |
Page 31 Summer 1991
|
A Notation for Juggling Tricks. A LOT of Juggling Tricks. By
Bruce Tiemann and Bengt Magnusson
From
time to time, jugglers come up with new patterns that look interesting,
and are relatively easy to do once you get the idea. But often
they're hard to explain or describe. There is a way. In this
article, a notation
will be presented that not only simplifies the description of
tricks, but also, because
of its mathematical basis, permits an analysis that generates
literally an infinite number of tricks.
Readers
familiar with a letter by Charlie Simpson, (JW,
Winter 86, p. 31) will find little new here as far as the
notation is concerned. One difference, though, is that instead of
using our notation merely to compile a library
of tricks, it can be used to generate all possible tricks
within certain constraints. To give credit where it is due, the
notation as presented here was independently (and previously)
invented by Paul Klimek, with whom we have had helpful discussions.
The
notation applies to one juggler with two hands, throwing alternately
left-right-Ieft-right in a steady pattern. However, it is easily
generalized beyond these constraints to passing patterns with any
number of hands, to multiplex patterns where more than one object is
thrown or caught at a time, and to in-sync patterns where the hands
throw together or in a syncopated rhythm. We welcome those
interested to pursue other applications.
The
notation here applies to throw heights relative to one another. It
is blind to the identity of the objects, applying equally to balls,
clubs, rings, or whatever. For the time being, we'll call them
balls. It is also blind to 'tricks" like backcrosses, Mills'
mess, under-the-Ieg throws or other such things where the throw
height (actually the away-from-hand time) is the same as it would
have been in the normal cascade.
In
other words, these examples aren't tricks in the sense that
something is changing from the notation's point of view - they are
all just the ordinary cascade. However, tricks such as the shower,
the half shower, the chase (three balls in a five pattern) and an
infinite number of similar yet distinct tricks exist that can be
done without the juggler making any kind
of funny throws - just by varying the throw heights between
consecutive throws.
In
this notation, a trick is represented by a string of numbers. Each
number in the string corresponds to one throw, e.g. a string of five
numbers represents five consecutive throws. Since the hands are
understood in this article to throw alternately, the first, third,
fifth, etc. numbers in the string apply to one hand, the rest apply
to the other.
The
value of the number dictates how high the throw is. It is
numerically equal to the number of balls that would be juggled if
every throw were that value. For
example, a 3 is the kind of throw made every time in a three
cascade, a rather low throw across from one hand to the other. A 4
is a somewhat higher throw (higher because the handspeed is
understood to be fixed at the three ball speed) that goes to the
same hand that threw it. A 5 is a rather high throw that crosses, a
6 is a very high throw that lands in the hand that threw it, etc.
Figures
one and two show the odd throws and the even throws up to 10 on the
same scale, which is for a six foot tall juggler making 2.5 throws
per second out of each hand, and assuming that catches in one hand
are exactly coincident with releases made from the other hand. (We
feel these are typical or representative values.) These figures can
be used to compare against other "juggletoons."
One other thing: the average of all the throw-height numbers in a trick is the same as the number of balls being juggled-which is obvious if all the throws have the same value, but is true in general. (More later.)
|

Figure
1- (left) The odd throws cross sides. The 1 throw is handed directly
from hand to hand. Figure 2- (right) The even throws land in the same hand that threw them. A tossed 2 would go up only two inches. |
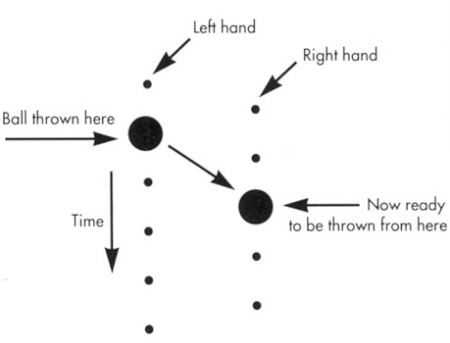
Figure 3---The diagram notation. This ball got a 3. |