How Many Objects Can Be Juggled - The Human Limits

by Jack Kalvan

I hate to break it to you aspiring numbers jugglers, but no human will ever 100 balls. Only a handful of people have reached a level to throw 11 or 12 objects into the air, and so far, not for more than few seconds. No one has even come come close to  juggling 13 balls. But is this within the realm of human possibility? 

Hand speed is one of the main factors that limit the number of objects one can juggle. (The other main factors being accuracy of throws and having long enough arms and enough space in the air for the juggling pattern.) I decided to find at anyone has the hand speed necessary to juggle 13 or more balls. So I designed a experiment to measure the theoretical human juggling limits - given the acceleration of the hands. 

To write the necessary equations, I define the following variables: 

b = number of balls 

h = number of hands 

f = flight time of a ball from throw to catch 

t = time between throws from the hand 

Vv = vertical throw velocity 

g = acceleration due to gravity = 9.81 m/s/s 

r = "dwell ratio" or fraction of time hand is holding a ball. My tests show r is usually about 2/3. 

W = average number of balls iri flight  per arc 

One can also think of r as the average number of balls in a hand while juggling. W can be expressed as the number of balls per hand minus the balls held in the hand.   W = (b / h) - r 

W is also equal to the time that balls are in flight divided by how often they are thrown: W = f  /  t . 

To simplify my analysis, I will assume balls are thrown and caught at the same height. Newtonian physics tells us the flight time of a ball, f = 2 Vv / g . Substituting this equations for f into the second equation for W gives W = 2 Vv / g / t . 

Since g is a constant, we see that W is proportional to the throwing velocity of the hand divided by the time between throws.  This means the number of balls in the air while juggling is closely related to the acceleration of the hand. Although a juggler's hands do not necessarily accelerate smoothly, the number of balls one can get into the air is approximately proportional to the maximum acceleration of one's hands 

I figured if I measure the maximum acceleration of a juggler's hands with a simple accelerometer, I could roughly calculate the juggler's maximum value for W.  And substituting this value into the equation, b / h = W, gives an approximation of the maximum number of balls one can theoretically juggle.  Remember, this maximum number of balls is calculated only from the speed a juggler can potentially throw balls into the air. It does not take into account accuracy of throws or the possibility of collisions. 

Since the number of balls juggled proportional to hand acceleration, a corollary is that the height of your juggling pattern is not related to your hand acceleration.  For example, if you juggle 5 balls high, you have about the same hand acceleration as if you juggle them low. The difference is that to  juggle high, you accelerate for a longer time and therefore have longer hand motion and a higher throwing velocity.

 I believe the following chart describes how the derivatives of the vertical hand motion relate to juggling: 

Vertical Hand Motion Derivatives - Tuesday February 17, 1998

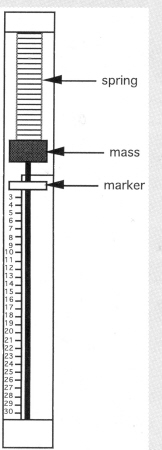
This simple device measures the hand acceleration. A small mass is connected to a spring inside a tube. When the hand accelerates the device (by shaking it up and down), two opposing forces act on the mass: the acceleration force (force = mass * acceleration) and the spring force ( force  = spring stiffness * distance stretched).  These forces are in equilibrium when the spring is stretched. A marker measures the maximum distance the spring was was stretched.  

Since the mass and spring stiffness are constant, the maximum acceleration is proportional to this distance. The distance the spring stretches is therefore proportional to the number of balls potentially juggled. 

To calibrate the device, I attached it to the back of a glove.  This method worked well for low numbers of balls but the glove and the weight of the jugglemeter made juggling more difficult.  Also imperfect juggling led to artificially high readings because more acceleration is needed to catch inaccurate throws.

To calibrate and test the jugglemeter for higher numbers of balls, I found it easiest to first juggle a number of balls long enough to get the feel of it.  Then, I'd drop the balls, pick up the jugglemeter and reproduce the same hand motions while holding it.  This process is not extremely accurate since it relies on the ability to reproduce the same hand motion as juggling but with the balls removed. However, after tests with many jugglers and up to 10 balls, and extrapolating the results, I feel confident that my calibration error is less than 10%.